01 题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是返回true，否则返回false。假设输入的数组的任意两个数字都互不相等。

二叉搜索树的概念：

二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。（摘自百度百科）

即左子树的值都小于根节点，右子树的值都大于根节点。左子树和右子树有着同样的规律。

举例如下图：

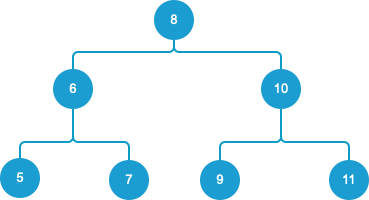
数组[5，7，6，9，11，10，8]是一个二叉搜索树的后序遍历数组。

02 解题

二叉搜索树的特性，左子树都小于根节点，右子树都大于根节点。

后续遍历的特性，根节点在最后被遍历。所以我们可以利用这两个特性解题。

数组5，7，6，9，11，10，8的判断过程如下

（1）首先确定根节点，最后一个元素 8

（2）从5开始遍历，寻找左子树节点。判断条件<根节点8

到9时，9>8,说明包含9以后的数都是8的右子树。记下9的数组下标i=3

假如9以后的数字有小于根节点8的情况，那么这个数组就不是二叉搜索树的后序遍历。

（3）遍历右子树判断，判断条件>根节点8

此次循环结束，左孩子都小于根节点，右孩子都大于根节点。

更新条件，继续重复上述遍历，判断左子树和右子树分别是否为二叉搜索树的后序遍历。

左子树

右子树

直到循环的树只有一个节点，或者树结构不是二叉搜索树结束。

03 代码和总结

代码

static boolean verifyPostOrder(int [] sequence, int start, int end) {
 int root = sequence[end];
 int i = start;
 // 1. 定位根节点的左子树，i的位置是分左子树右子树分界线。
 for (; i < end; i ++) {
 if (sequence[i] > root) {
 break;
 }
 }
 // 2. 判断根节点的右树节点是否存在小于根节点节点。
 for (int j = i; j < end; j ++ ) {
 if (sequence[j] < root) {
 return false;
 }
 }
 // 3.继续左子树右子树的判断
 boolean left = true;
 if (start < i - 1) {
 left = verifyPostOrder(sequence, start, i - 1);
 }
 boolean right = true;
 if (i < end - 1) {
 right = verifyPostOrder(sequence, i, end - 1);
 }
 //4.左子树和右子树都为二叉搜索树后续遍历结果，才返回true
 return left & right;
}

测试代码

public static void main(String[] args) {
 int []sequence = new int[]{5,7,6,9,11,10,8};
 System.out.println(verifyPostOrder(sequence, 0, sequence.length - 1));
 int []sequence1 = new int[]{7,4,6,5};
 System.out.println(verifyPostOrder(sequence1, 0, sequence1.length - 1));
}